在x轴上的双曲线:a表示双曲线右支的顶点位置,c表示焦点位置,b表示虚轴的一半。以OF2为直径的圆与以OA为半径的圆交于P,则|OP|=|OA|=a,|PF2|=√(c^2-a^2)=b。

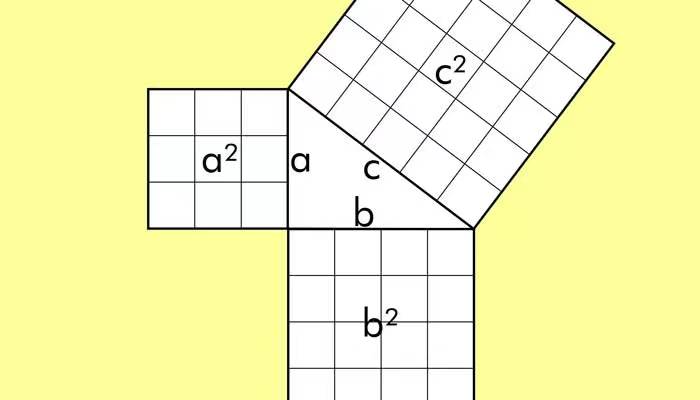
对于双曲线a为原点到与x轴交点,c为原点到与焦点的距离,a^2+b^2=c^2,渐近线与x轴还有过双曲线与x轴交点,并垂直于x轴的直线组成的,一个直角三角形的条边分别对应a、b、c。
双曲线有两个焦点,两条准线。(注意:尽管定义2中只提到了一个焦点和一条准线,但是给定同侧的一个焦点,一条准线以及离心率可以根据定义2同时得到双曲线的两支,并且两支关于虚轴对称。所以在两侧的焦点,准线和相同离心率得到的双曲线是相同的。)

在标准方程中令x=0,得y²=-b²,该方程无实根,为便于作图,在y轴上画出B1(0,b)和B2(0,-b),以B1B2为虚轴。





